2.7 アルゴリズム4 決定木
- このセクションのためにはgraphvizをインストールしておく必要がある。
pip install graphviz以外に、別途OSに応じた方法でgraphvizをインストール。- ubuntuならば
sudo apt-get install graphviz。
- 回帰にも分類にも使える。
- Yes/Noで答えられる質問で出来た木を構成する。
mglearn.plots.plot_animal_tree()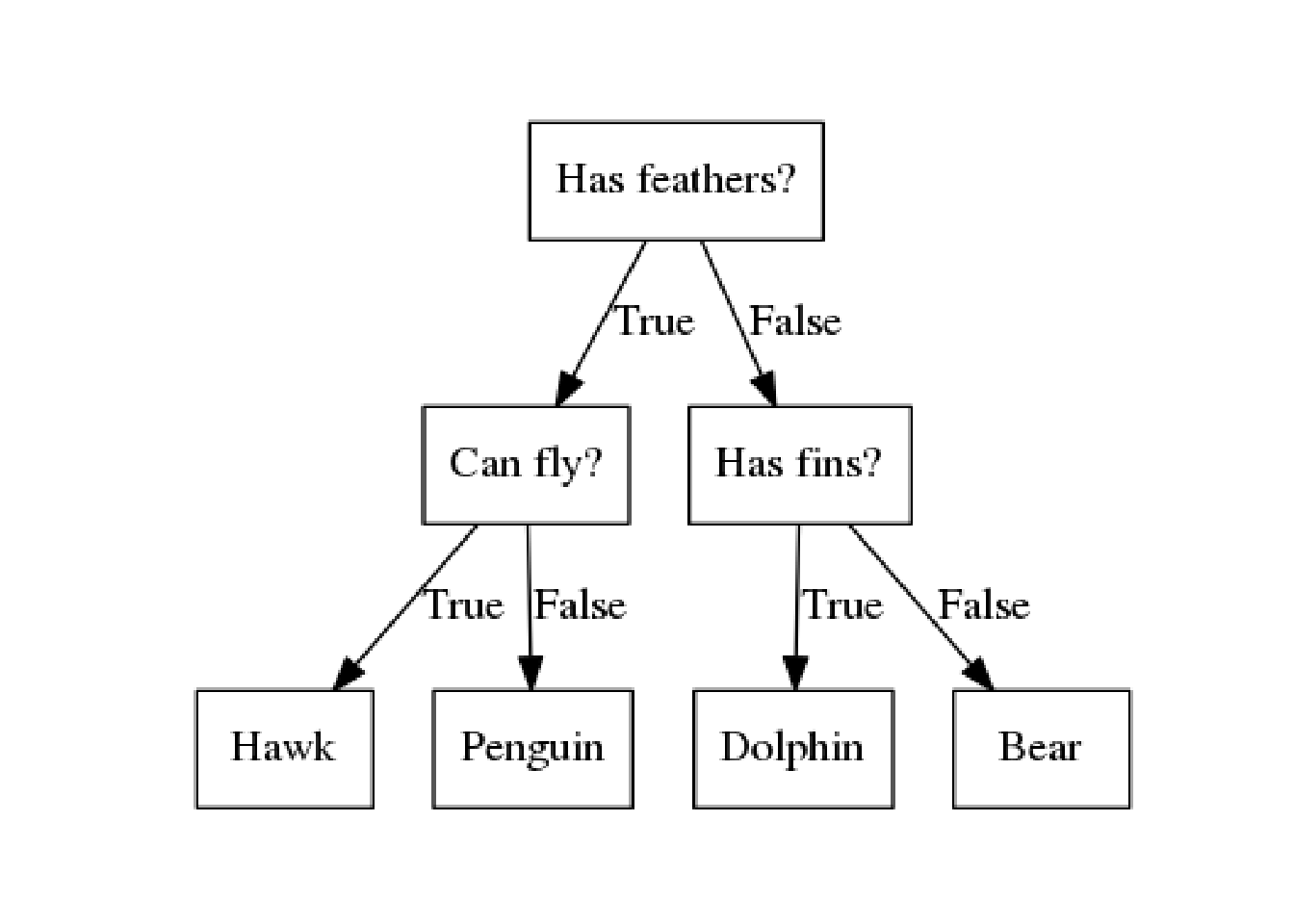
2.7.1 決定木の構築
- 2つの特徴量、2つのクラスを持つデータセットtwo_moonを使用する。
- 2つの特徴量のなす平面上で2つのクラスが半月を組合せたように分布している。
from sklearn.datasets import make_moons
from mglearn.tools import discrete_scatter
X, y = make_moons(n_samples=100, noise=0.25, random_state=3)
plt.figure()
ax = plt.gca()
discrete_scatter(X[:, 0], X[:, 1], y, ax=ax)
ax.set_xticks(())
ax.set_yticks(())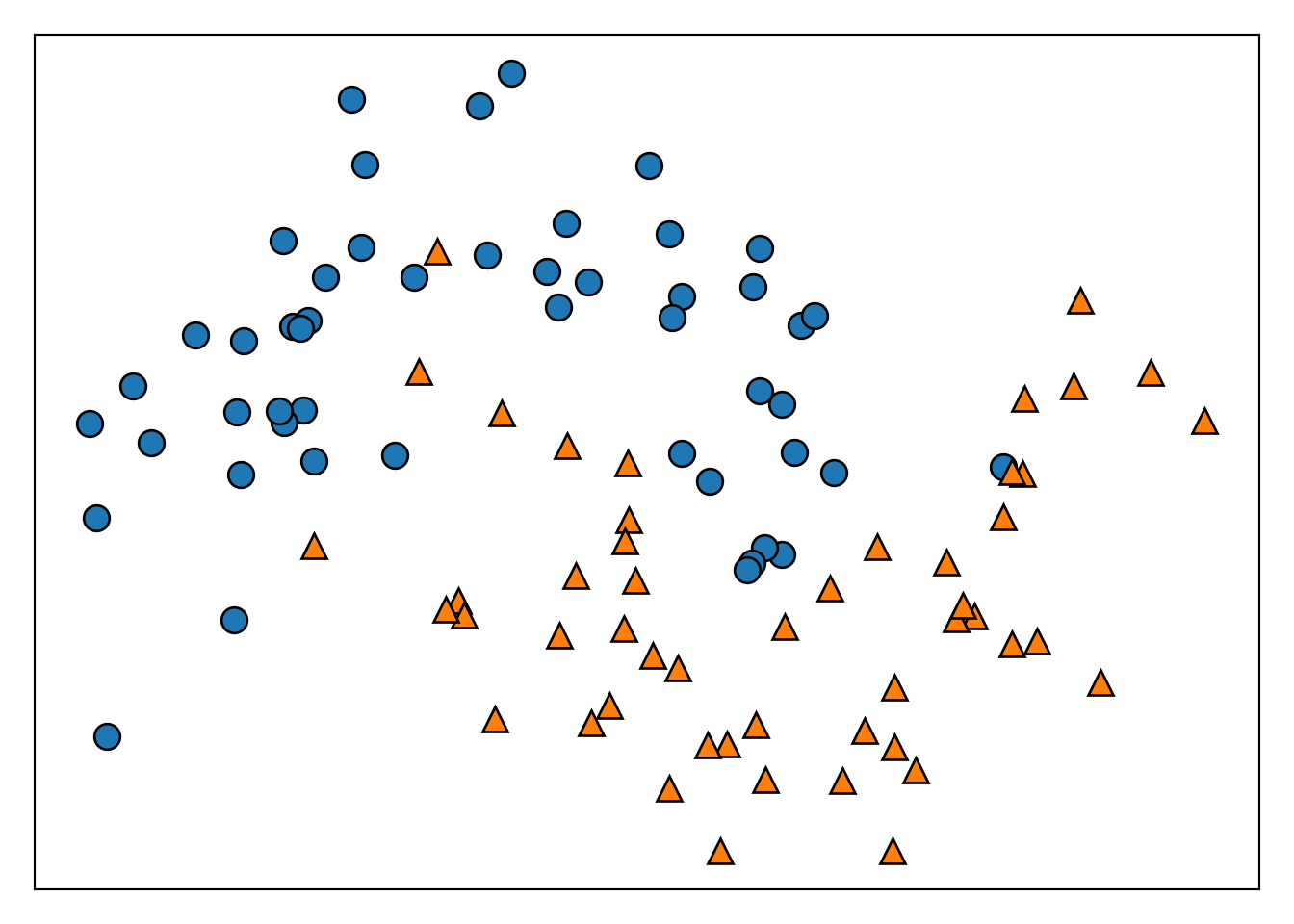
- 木の構築は、データセットの分割の繰り返しである。分割された部分を葉と呼ぶ。
- 分割によりテストが1段階増える(e.g. X[1]は0.06以上であるか?)
- 各ステップで分割は情報量が最も多くなるように(最もクラスを分割するように)行われる。
- 分割はテストによってデータセットが完全に分類できるようになるまで進む。
- 1つの葉に1種類のクラスや値しか含まない状態になった木を純粋(pure)と呼ぶ。
以下にtwo_moonから純粋な決定木を作成する過程を示す。
for i, max_depth in enumerate([1, 2, 9]):
fig, ax = plt.subplots(1, 2, figsize = (12, 4), subplot_kw={'xticks': (), 'yticks': ()})
tree = mglearn.plot_interactive_tree.plot_tree(X, y, max_depth = max_depth, ax = ax[0])
ax[1].imshow(mglearn.plot_interactive_tree.tree_image(tree))
plt.show()
plt.close()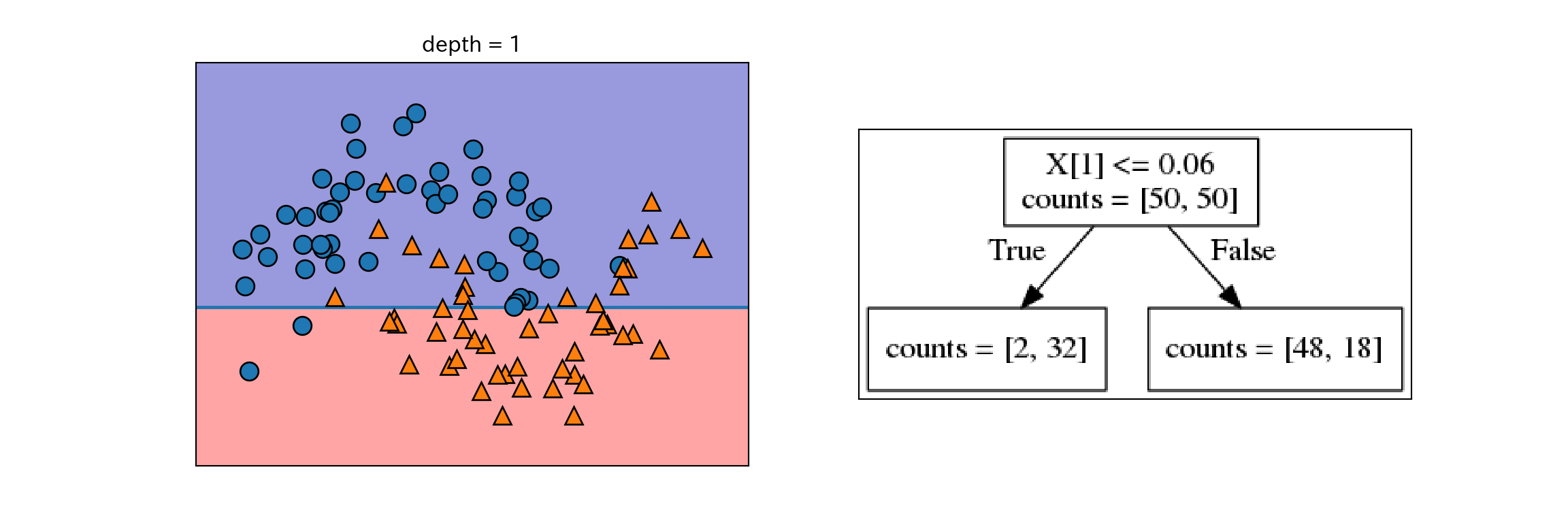
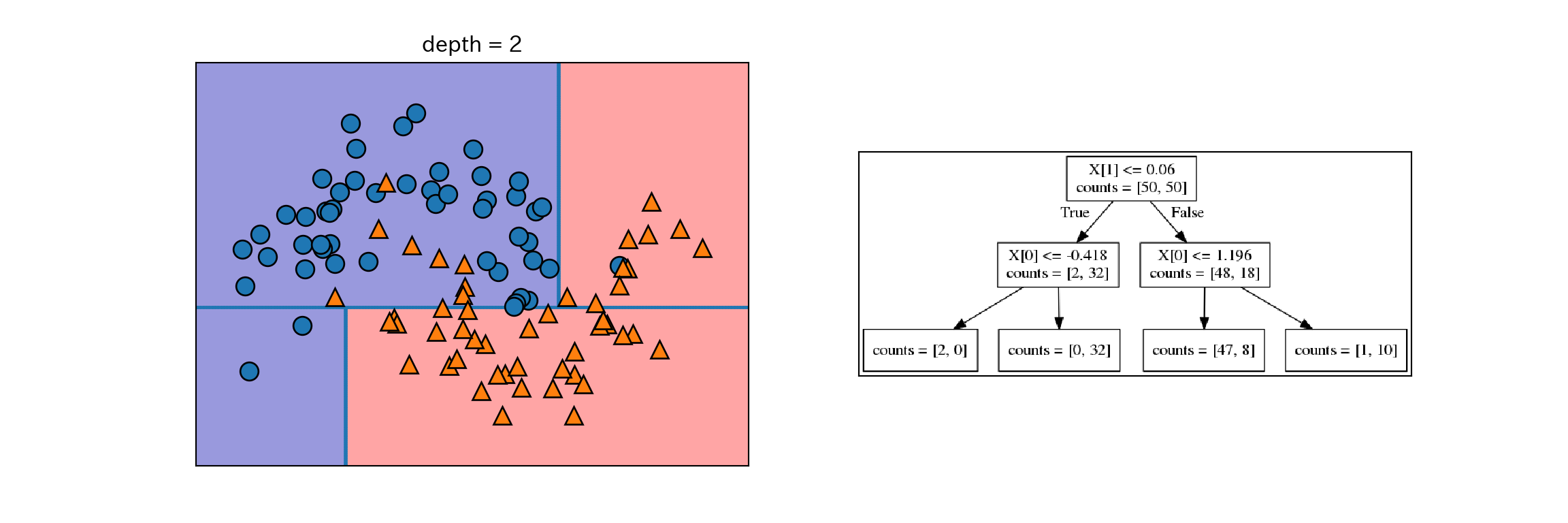
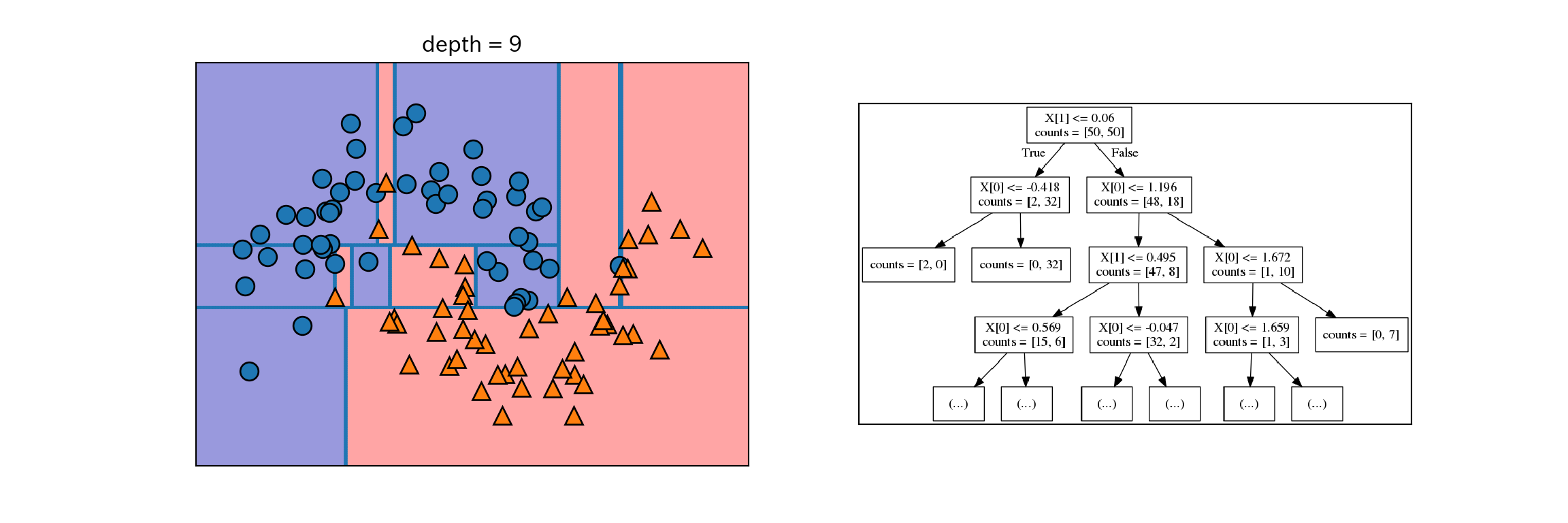
決定木はターゲットがクラスではなく連続値になっても同じように機能するので、回帰にも使える。
2.7.2 決定木の複雑さの制御
- 純粋になるまで分割を続けるとルールが複雑になりすぎ、容易に過剰適合してしまう。
- 過剰適合を防ぐ戦略は2つある。
- 事前枝刈り: 構築過程で木の生成を止める。単に枝刈りとも。
- 木の深さを制限する方法、葉の最大値を制限する方法、葉に含まれるデータ点の最小数を制限する方法がある。
- scikit-learnには事前枝刈りしか実装されていない。
- 事後枝刈り: 木を構築してから情報量の少ない枝を削除する。
- 事前枝刈り: 構築過程で木の生成を止める。単に枝刈りとも。
- scikit-learnの決定木の実装
- 回帰: DecisionTreeRegressorクラス
- 分類: DecisionTreeClassifierクラス
以下ではcancerデータに対して決定木を作成し、枝刈りの効果を確認する。まずはデフォルトの設定で訓練セットに対して木を構築する。デフォルトでは葉が純粋になるまで分類する。
from sklearn.tree import DecisionTreeClassifier
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, stratify=cancer.target, random_state = 42
)
tree = DecisionTreeClassifier(random_state = 0) # 内部でタイブレークの判定に使う乱数を固定している
tree.fit(X_train, y_train)
print("訓練セットに対する精度:{:.3f}".format(tree.score(X_train, y_train)))
## 訓練セットに対する精度:1.000
print("テストセットに対する精度:{:.3f}".format(tree.score(X_test, y_test)))
## テストセットに対する精度:0.937- 葉が純粋になるまで分割しているので、訓練セットに対する精度は当然1になる。
- テストセットに対する制度は線形モデルの例で見た時より若干低い。
次に、枝刈りの例として木の深さを4に固定してみる。
tree = DecisionTreeClassifier(max_depth = 4, random_state = 0)
tree.fit(X_train, y_train)
print("訓練セットに対する精度:{:.3f}".format(tree.score(X_train, y_train)))
## 訓練セットに対する精度:0.988
print("テストセットに対する精度:{:.3f}".format(tree.score(X_test, y_test)))
## テストセットに対する精度:0.951訓練セットに対する精度と引き換えに、汎化性能が向上していることが分かる。
2.7.3 決定木の解析
- 木の可視化のために、まずは
treeモジュールのexport_graphviz関数でグラフを書き出す。 - 出力はグラフに対応するファイル形式である.dot形式のファイル。
from sklearn.tree import export_graphviz
export_graphviz(
tree, out_file = "output/tree.dot", class_names = ["malignant", "benign"],
feature_names = cancer.feature_names, impurity = False, filled = True
)- .dotファイルの可視化はgraphvizモジュールで行う
import graphviz
from PIL import Image
with open("output/tree.dot") as f:
dot_graph = f.read()
g = graphviz.Source(dot_graph)
g.format = "png"
g.render("output/tree.gv")
img = np.array(Image.open("output/tree.gv.png"))
plt.imshow(img)
plt.axis('off')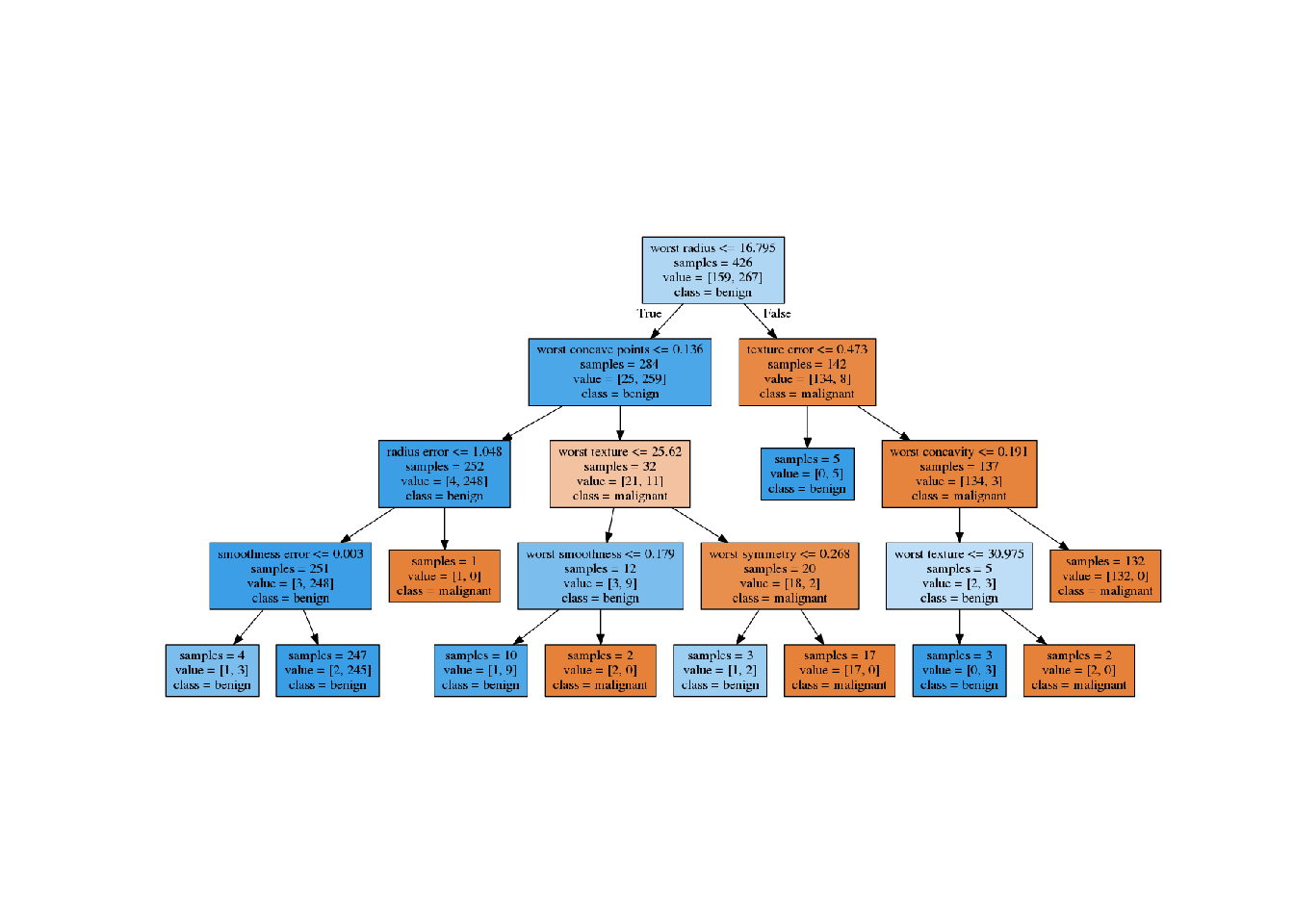
可視化した木は多くの情報を含むが、特に大部分のデータが通るパスはどこか?に注目すると良い。
2.7.4 決定木の特徴量の重要性
決定木全体を確認し、把握するのは大変な作業なので、以下のような情報が使用される場合がある。
- 特徴量の重要度 (feature importance) 個々の特徴量はそれぞれの判断に対してどの程度重要なのか?
- 1に近いほど重要。1であればその特徴量だけで完全に判別ができるということ。
- 0に近いほど重要ではない
特徴量の重要度はフィット済みオブジェクトの.feature_importance_に格納されている。
print(tree.feature_importances_)
## [0. 0. 0. 0. 0. 0.
## 0. 0. 0. 0. 0.01019737 0.04839825
## 0. 0. 0.0024156 0. 0. 0.
## 0. 0. 0.72682851 0.0458159 0. 0.
## 0.0141577 0. 0.018188 0.1221132 0.01188548 0. ]このままではわかりにくいのでプロットしてみる。
n_features = cancer.data.shape[1]
plt.barh(range(n_features), tree.feature_importances_, align = 'center')
plt.yticks(np.arange(n_features), cancer.feature_names)
plt.xlabel("特徴量の重要度")
plt.ylabel("特徴量")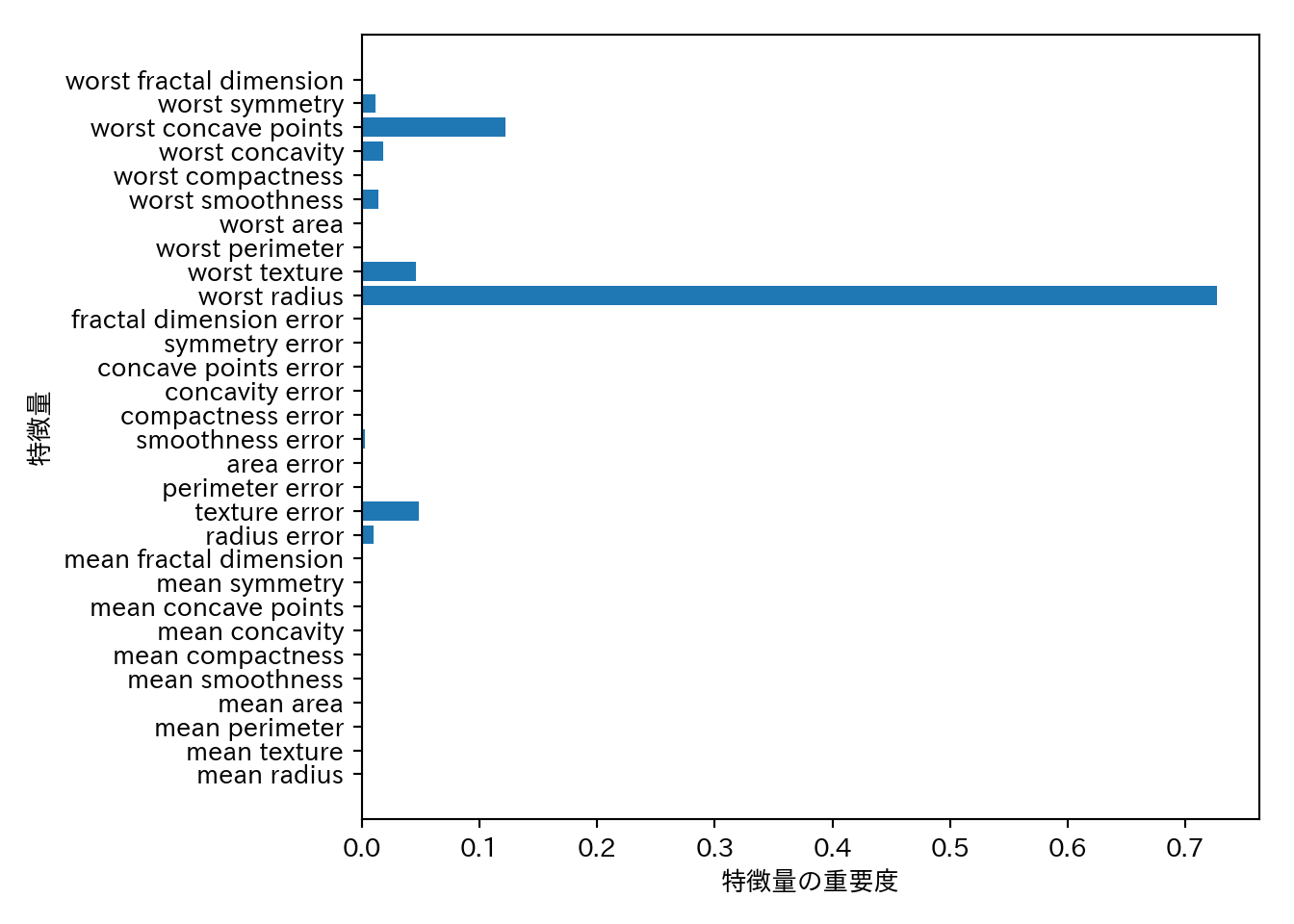
- 特徴量の重要度が高い特徴量は重要だが、逆は必ずしも成り立たないという点に注意が必要である。
- 特徴量間に強い相関があり、いずれかの特徴量で十分説明出来てしまう場合は、残りの特徴量がたまたま採用されないということがありうる。
- 特徴量の重要度は係数と異なって常に正であり、その特徴量が大きいとクラスがどれになるのかは直接は分からない。
- 上記の例ではworst radiusは少なくとも重要だが、他に重要な特徴量がある可能性は除外できないし、worst radiusの値と良性・悪性の関係がどのようになっているのかも自明ではない。
そもそも、特徴量とクラスの関係は必ずしも単純とは限らない。例えば次のような2つの特徴量からなる2クラス分類問題を考えてみる。この例は、クラスを分けるルールは単純で明確だが、クラス1はクラス0の中に分布しているので、一定の大小関係だけでは分類できない。
tree = mglearn.plots.plot_tree_not_monotone()
## Feature importances: [0. 1.]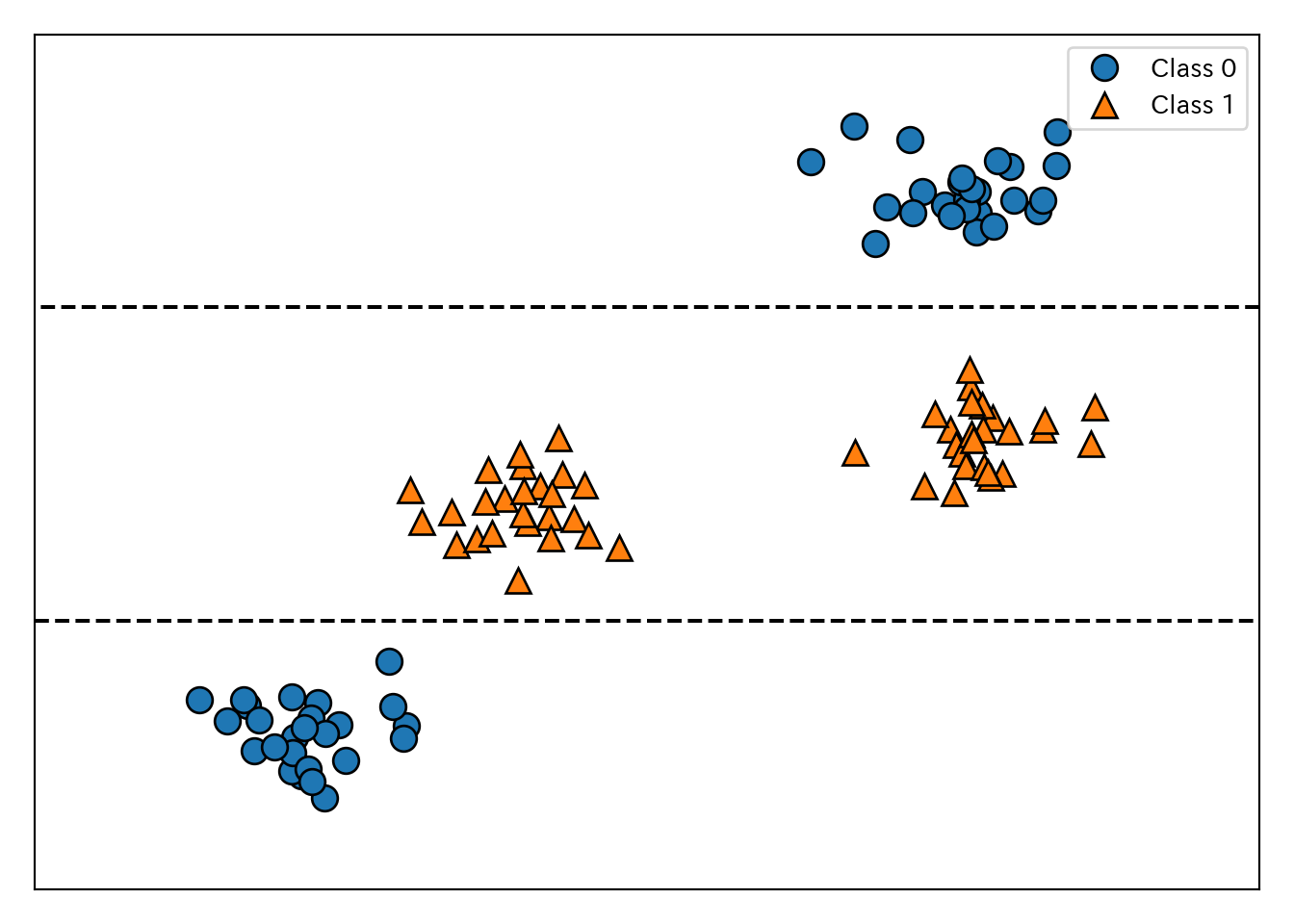
tree.format = "png"
tree.render("output/not_monotone.gv")
img = np.array(Image.open("output/not_monotone.gv.png"))
plt.imshow(img)
plt.axis('off')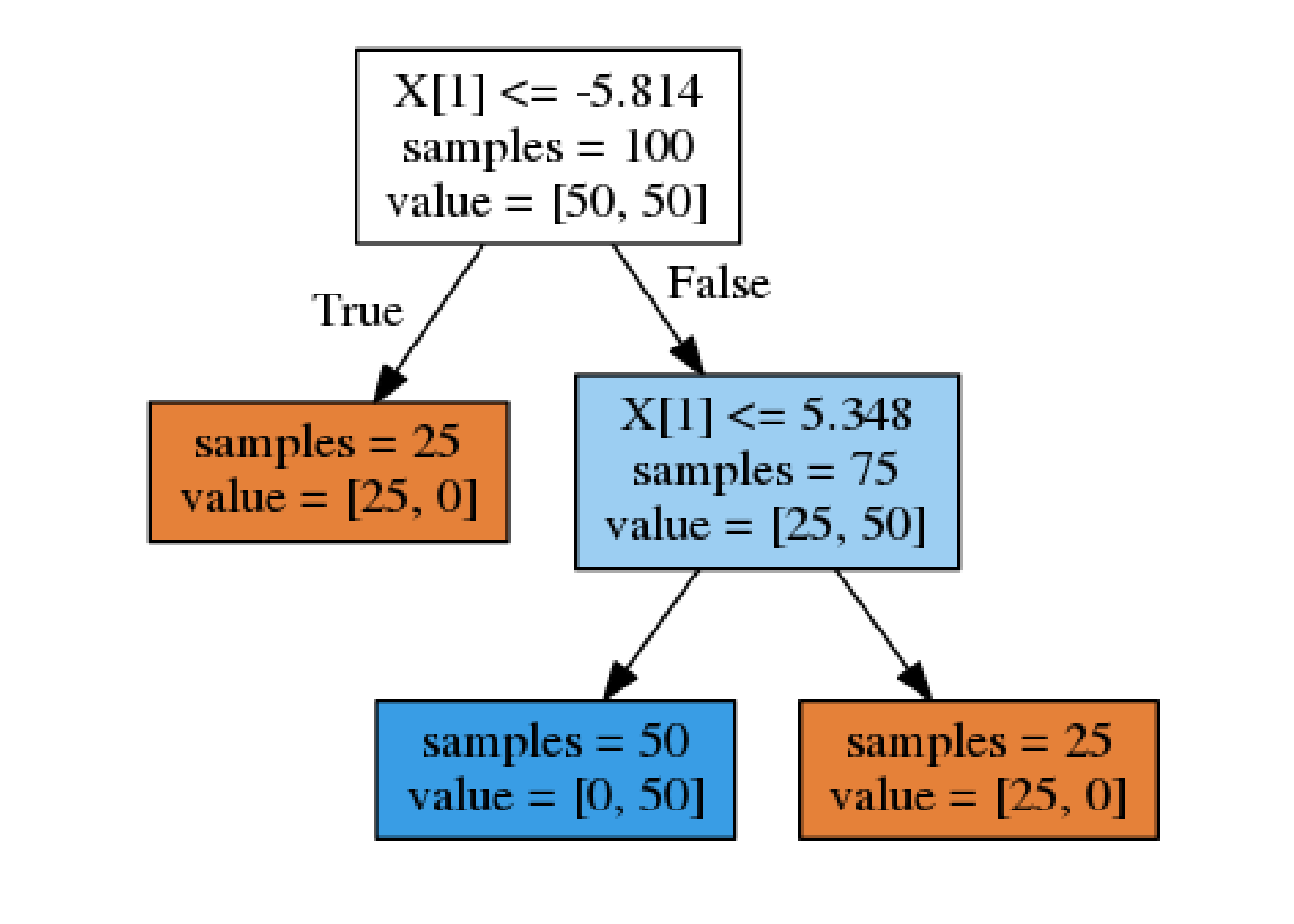
- 決定木による分類の議論は決定木による回帰にも当てはまる。
- 決定木による回帰では、外挿 (extrapolate)ができない点に注意する。
決定木は外挿ができないという点について、RAM価格の推移データセットを使って例を示そう。
import os
ram_prices = pd.read_csv(os.path.join(mglearn.datasets.DATA_PATH, "ram_price.csv"))
plt.semilogy(ram_prices.date, ram_prices.price)
plt.xlabel("年")
plt.ylabel("1Mバイトあたりの価格($)")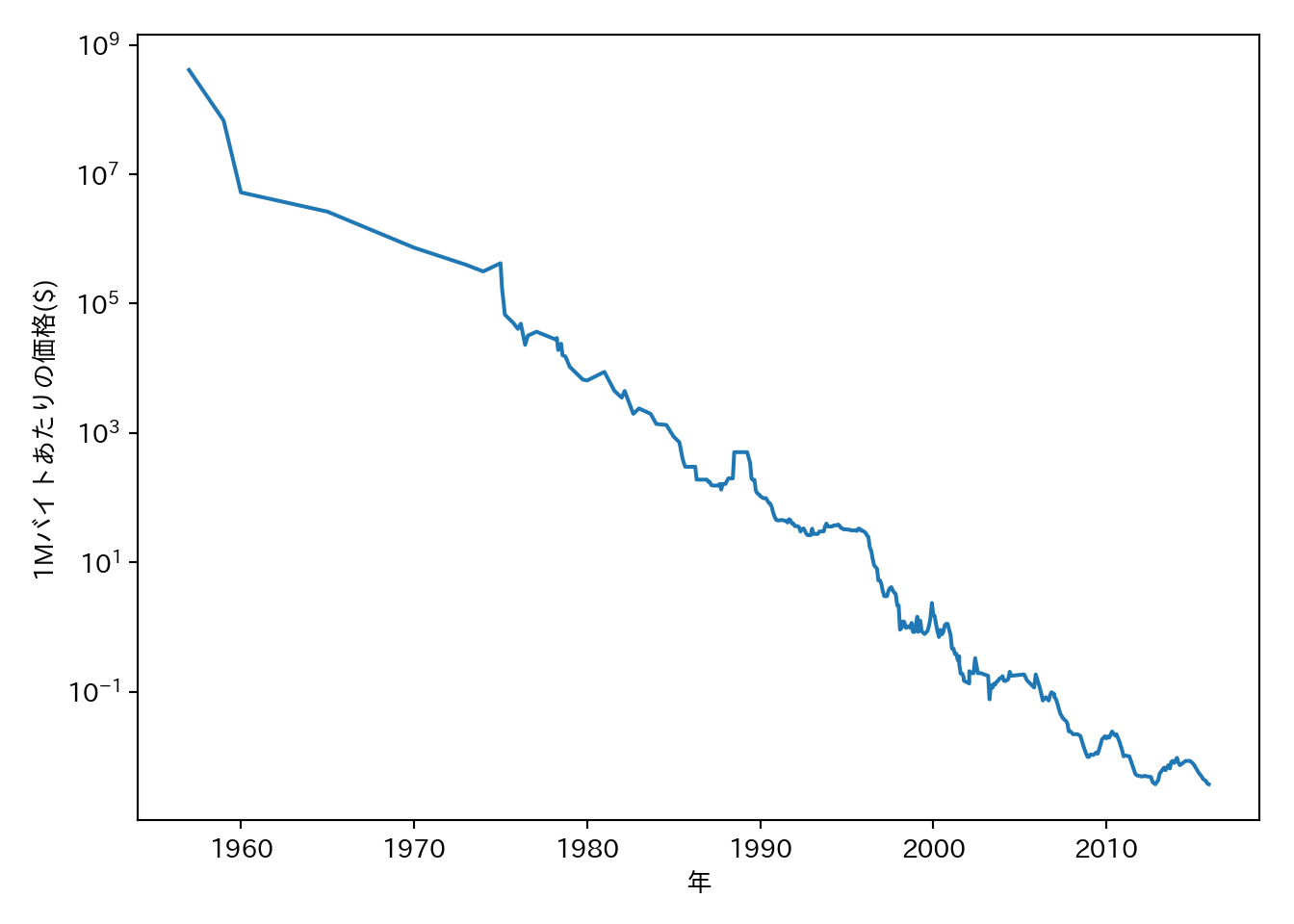
関係を直線的にするために、価格を対数変換しているという点に注意してもらいたい。この種の変換は線形回帰を行う際に重要となる。
データセットに対し、線形回帰と回帰木を適用する。ここでは、2000年より前のデータを訓練セットとし、2000年以降のデータをテストセットとする。つまり、過去のデータから将来を予測する。
from sklearn.tree import DecisionTreeRegressor
data_train = ram_prices[ram_prices.date < 2000]
data_test = ram_prices[ram_prices.date >= 2000]
X_train = data_train.date[:, np.newaxis]
y_train = np.log(data_train.price) #対数変換
# モデルに訓練データをフィットさせる
tree = DecisionTreeRegressor().fit(X_train, y_train)
linear_reg = LinearRegression().fit(X_train, y_train)
# 2000年以降も含めた全てのデータポイントに対して予測を行う
X_all = ram_prices.date[:, np.newaxis]
pred_tree = tree.predict(X_all)
pred_lr = linear_reg.predict(X_all)
price_tree = np.exp(pred_tree) #対数変換を解除
price_lr = np.exp(pred_lr)
## プロット
plt.semilogy(data_train.date, data_train.price, label = "訓練データ")
plt.semilogy(data_test.date, data_test.price, label = "テストデータ")
plt.semilogy(ram_prices.date, price_tree, label = "回帰木")
plt.semilogy(ram_prices.date, price_lr, label = "線形回帰")
plt.legend()plt.tight_layout()
plt.show()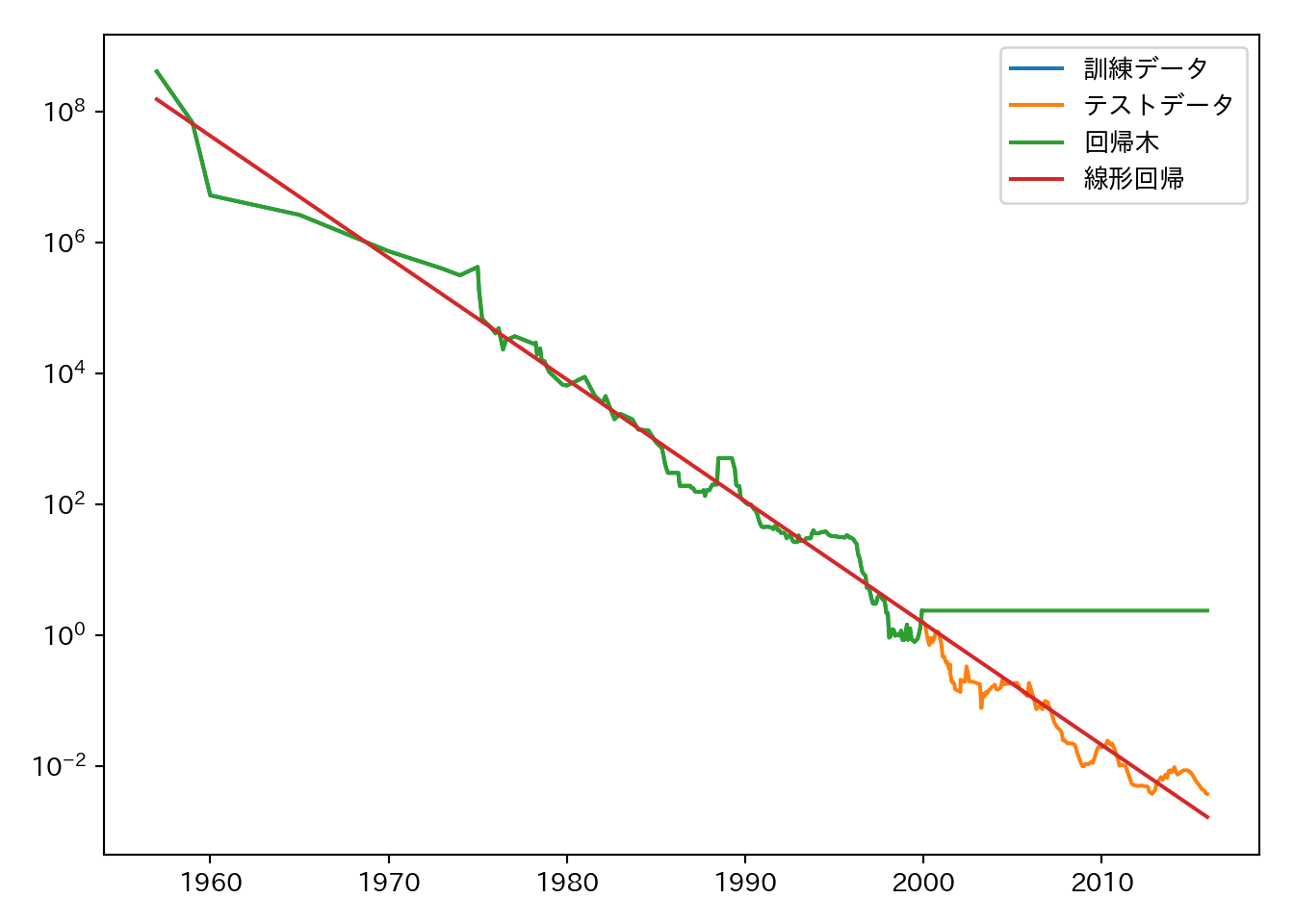
plt.close()線形回帰は2000年以降の値も予測出来ているのに対して、回帰木は単に2000年の値を返すだけになっている。
2.7.5 長所、短所、パラメータ
- 決定木のパラメータは事前枝刈りに関するパラメータである。
- 大抵の場合はmax_depth、max_leaf_nodes、min_samples_leafのいずれか1つの指定で十分である。
- 決定木は容易に可視化可能であり、理解しやすい。
- 決定木の分割は特徴量毎に行われるため、特徴量を正規化したり標準化したりする必要はない。
- 特徴量の最大の欠点は事前枝刈りを行ったとしても過剰適合しやすく、汎化性能が低くなりやすいという点である。