Project Eulerの話

# Project Eulerの話
### <span class="citation">@nozma</span>
### 2019-04-05

---

# 最近AtCoderはじめました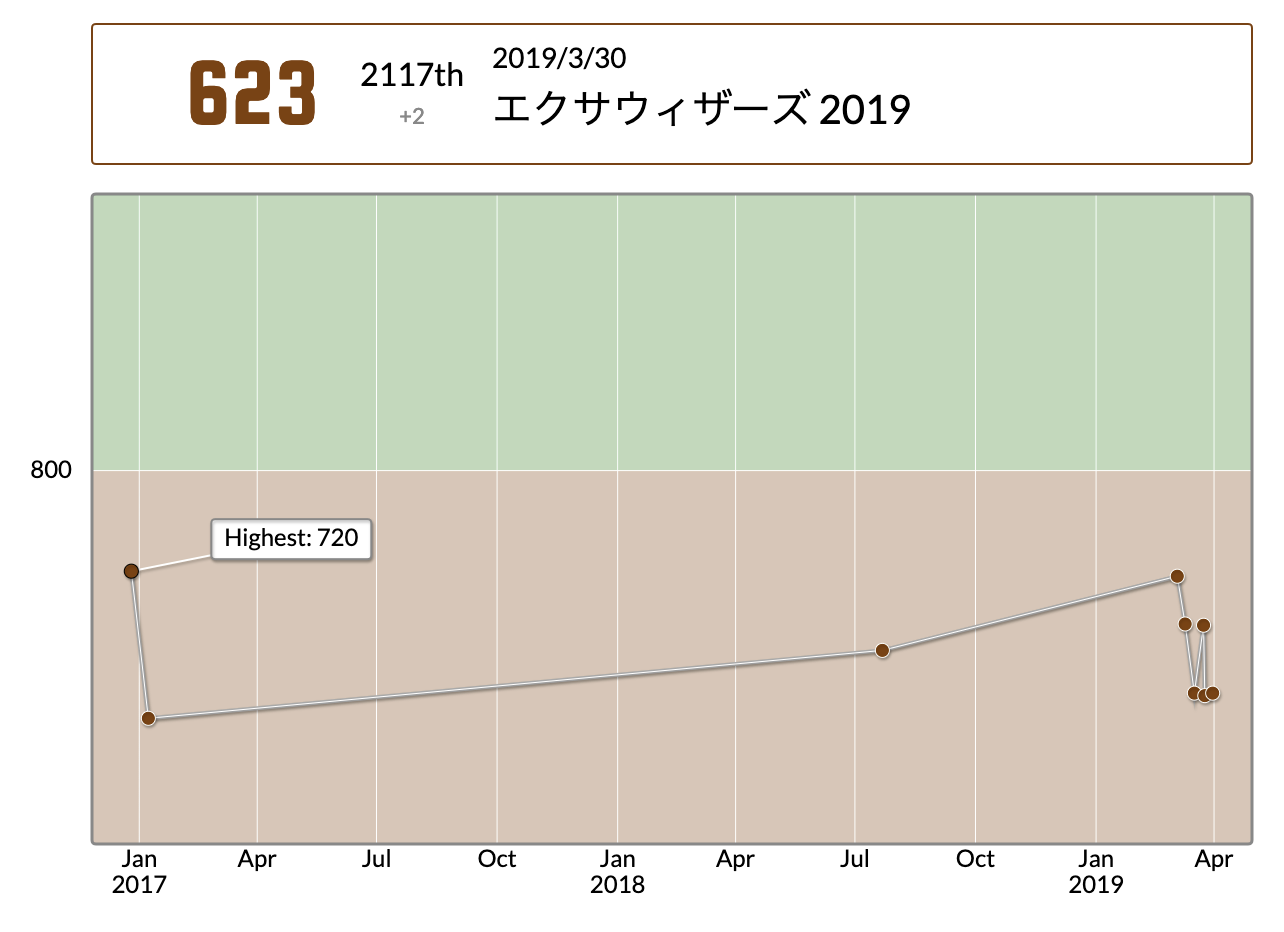

![:scale 50%](fig/ac_progress.png)

まだクソザコナメクジ。

---

# 実は深刻な問題があります

---

# Rが使えない…

---

# Rが使えない…!!

---

## Rを！！！！！！！！！！
## 使わせろ！！！！！！！

---

# プロコンあるある

- Rが使えない（重要）
- バージョンが古い
- 好きなライブラリを使えない
- Rが使えない（重要）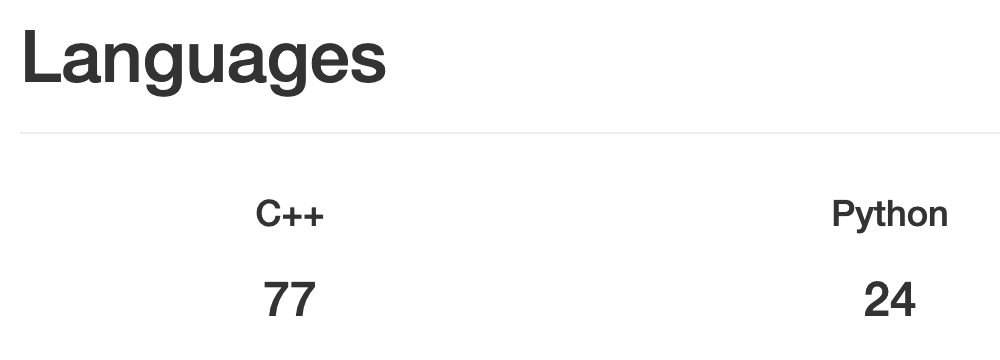

![:scale 30%](fig/ac_languages.png)

---

# そんな私に

---

# 誰？

---

# 何？

数学の問題集です。

コンピュータを用いて計算することが想定されています。

---

## Project Eulerのここがすごい

#### ルールが簡単

- n桁の数字を解答欄に書き込むだけ（n=ﾁｮｯﾄ）

#### 時間に制限がない

- **1分以内に解ける**ように設計されている（one-minute rule）

#### ググっても良い

- むしろ推奨されている

---

## Project Eulerのここがすごい

#### （たまに）解説PDFがある

- （実際あんまりない）

#### フォーラムがある

- 時間をかけて解く -> フォーラムで賢いやり方を学ぶというのが一般的

#### 言語に制限がない

- 手元で実行なので当然

---

### 言語に制限がない！！！

---

### どんな言語が使われているのか？

AtCoderとProject Eulerでそれぞれ集計してみました。

---

### AtCoderのランキング

- APIがあったのでそこからデータ取得
    - [kenkoooo/AtCoderProblems: Problem manager for AtCoder users](https://github.com/kenkoooo/AtCoderProblems/)
    - jsonを`rlist`パッケージで読み込んで加工
- 次の項目を計算してグラフを作成
    - ユーザー数 ... ACが1件以上あればユーザとカウント
    - AC平均 ... Accepted合計 / ユーザー数

---

AtCoderの使用言語ランキング

![:scale 50%](fig/ac_total.svg)

---

AtCoderのつよい言語ランキング

![:scale 50%](fig/ac_rank.svg)

---

### Project Eulerのランキング

- [Statistics - Project Euler](https://projecteuler.net/languages)に統計情報があるので取得
    - 認証が必要なので`RSelenium`パッケージでログイン
    - `rvest`でスクレイピング
- 次の情報があるので可視化（件数が多いので上位50%のみ）
    - ユーザー数...ユーザーがプロフィールで設定するもの
    - 回答率...回答数/問題数が言語別に集計されたもの

---

Project Eulerの使用言語ランキング

![:scale 50%](fig/euler_total.svg)

---

つよい言語ランキング

![:scale 50%](fig/euler_rank.svg)

---

# やってみよう

---

## Problem 1 -- Multiples of 3 and 5

> 3か5で割り切れる1000未満の自然数の合計は何か？

PE版のfizzbuzzです。

---

# PE001 回答例

---

## 素直に解く

```r
ans <- 0
for (i in seq_len(999)) {
  if (i %% 3 == 0 | i %% 5 == 0) {
    ans <- ans + i
  }
}
```

良いと思います。

---

## もっとFizzBuzzっぽく

```r
sum((x=1:999)[!(x%%3&x%%5)])
```

書き方にこだわってみても良いでしょう。

---

## もっと最近のRっぽく

```r
library(dplyr)
data.frame(x = 1:999) %>% 
  filter(x %% 3 == 0 | x %% 5 == 0) %>% 
  summarise(answer = sum(x))
```

好きなライブラリを使ったって良いんです。

---

## Pythonが使いたいんじゃ

```python
print(sum(i for i in range(1000) if i % 3 == 0 or i % 5 == 0))
```

どうしてもPythonが良いというなら止めません。

---

#### ~~あまり役に立たない~~知見が得られる問題が盛りだくさんです

---

### Problem 92 Square digit chains

>「各桁の値の2乗の合計を計算する」という操作を繰返します。
> - 44 -> 32 -> 13 -> 10 -> **1** -> **1**
> - 85 -> **89** -> 145 -> 42 -> 20 -> 4 -> 16 -> 37 -> 58 -> **89**
>
> 1つめの例では、1に到達し、2つめの例では89から始まるループに到達しています。実は、操作を繰り返すと**すべての自然数は1または89に到達します**。<br />1千万以下の自然数のうち、89に到達する数はいくつあるでしょうか？

---

### 考え方

- 上限をN、ループ判定に必要な時間をMとして `$O(N \times M)$` 程度の計算量が必要です。
- N = 1e7なので、Mの値次第では結構時間がかかります。
- どうするか？（考えてみましょう）

- ヒント：ほぼ `$O(N)$` の解法があります

---

### 回答例

- 「2乗の和」の計算結果は、最大でも `$9^2*6 = 486$` です
- すべての値について1回だけ処理をすれば、すべて486以下の値になります。
- したがって486以下の整数について**最終的に89になるのか？**を把握しておき、配列などにメモっておけば高速に計算できます。

---

class:center, middle

### Project Eulerのここがすごい

#### 日常生活で比較的使わない概念を知ることができます

---

### Q. 何？

## `$3 \upuparrows 3$`

---

### 答: テトレーション

## `$3 \upuparrows 3 = 3^{3^3} = 3^{27} = 7,625,597,484,987$`

cf. 大きな数が好きなら[寿司 虚空編](https://comic.pixiv.net/viewer/stories/6994)を読もう!

---

### Problem 188

`$1777 \upuparrows 1855$`の下8桁を求めよ。

- ヒント1: 桁だけでメモリが死ぬので直接計算してはいけません

- ヒント2: 冪乗演算子は右結合なので左から計算してはいけません

```r
# これではダメです
n <- 1777
for (i in 1:1855) n <- n^1777 mod 1e8
```

---

### オイラーの定理

`$a$` と `$n$` を互いに素な正整数とします。このとき次の関係が成立します。

$$ a^{\varphi(n)} \bmod n = 1 $$

`$\varphi(n)$` はオイラーの `$\varphi$` （トーシェント）関数というもので、 `$n$` 以下の自然数で `$n$` と互いに素な自然数の個数を返します。

例) `$n = 6$` なら1と5が互いに素なので `$\varphi(6) = 2$`。 `$a=5$`とすると、 `$5^2 \bmod 6 = 1$`となってオイラーの定理が成り立つ。

---

### で？

1777は素数なので、1e8と互いに素です。つまり次の関係が成り立ちます。

$$ 1777^{\varphi(10^8)} \bmod 10^8 = 1 $$

`$\varphi(10^8) = 4 \times 10^7$` 乗する度に下8桁が00000001に戻るということです。つまりこうです。

$$ 1777^x \bmod 10^8 = 1777^{x \bmod 4 \times 10^7} \bmod 10^8$$

指数部分の剰余をとってから計算して良いということです。

---

### コードにするとこう

```r
solve <- function(a, b, m) {
  ans = 1
  for (i in seq_len(b)) {
    if (i == b) m = 1e8
    ans = modpow(a, ans, m)
  }
  return(ans)
}
solve(1777, 1855, 4e7)
```

※冪乗の剰余を計算する関数がRには無いので適当に定義する必要があります。メンドイ!!

---

### 実は…

- ループは10回で良い
- `$10^8$` で剰余とっても良い
- Pythonだと楽

```python
x = 1
for i in range(10):
  x = pow(1777, x, 10**8)
print(x)
```

とかいろいろあって~~闇が~~奥が深いです。問題解いてからforum覗いてみるとよいでしょう。

---

### 終